#数据处理部分之前的代码，保持不变 import os import random import paddle import numpy as np 

import matplotlib.pyplot as plt from PIL import Image import gzip import json import warnings 
warnings.filterwarnings('ignore') import paddle.nn as nn from paddle.nn import Conv2D, MaxPool2D,

 Linear import paddle.nn.functional as F # 创建一个类MnistDataset，继承paddle.io.Dataset 这个类 #

 MnistDataset的作用和上面load_data()函数的作用相同，均是构建一个迭代器 class MnistDataset(paddle

.io.Dataset): def __init__(self, mode): datafile = './work/mnist.json.gz' data = json.load(gzip.

open(datafile)) # 读取到的数据区分训练集，验证集，测试集 train_set, val_set, eval_set = data #

 数据集相关参数，图片高度IMG_ROWS, 图片宽度IMG_COLS self.IMG_ROWS = 28 self.IMG_COLS = 28 if mo

de=='train': # 获得训练数据集 imgs, labels = train_set[0], train_set[1] elif mode=='valid': # 

获得验证数据集 imgs, labels = val_set[0], val_set[1] elif mode=='eval': # 获得测试数据集 imgs, 

labels = eval_set[0], eval_set[1] else: raise Exception("mode can only be one of ['train', '

valid', 'eval']") # 校验数据 imgs_length = len(imgs) assert len(imgs) == len(labels), \ "length

 of train_imgs({}) should be the same as train_labels({})".format(len(imgs), len(labels))
        
        self.imgs = imgs
        self.labels = labels def __getitem__(self, idx): # MLP # img = np.array(self.imgs[idx]).

astype('float32') # label = np.array(self.labels[idx]).astype('int64') # CNN img = np.reshape(self

.imgs[idx], [1, self.IMG_ROWS, self.IMG_COLS]).astype('float32')
        label = np.reshape(self.labels[idx], [1]).astype('int64') return img, label def __len__

(self): return len(self.imgs) # 定义模型结构 class MNIST(paddle.nn.Layer): def __init__(self)

: super(MNIST, self).__init__()
         nn.initializer.set_global_initializer(nn.initializer.Uniform(), nn.initializer.Constant()) 

# 定义卷积层，输出特征通道out_channels设置为20，卷积核的大小kernel_size为5，卷积步长stride=1，

padding=2 self.conv1 = Conv2D(in_channels=1, out_channels=20, kernel_size=5, stride=1, padding=2) 

# 定义池化层，池化层卷积核kernel_size为2，池化步长为2 self.max_pool1 = MaxPool2D(kernel_size=2,

 stride=2) # 定义卷积层，输出特征通道out_channels设置为20，卷积核的大小kernel_size为5，卷积步长s

tride=1，padding=2 self.conv2 = Conv2D(in_channels=20, out_channels=20, kernel_size=5, stride=1, 

padding=2) # 定义池化层，池化层卷积核kernel_size为2，池化步长为2 self.max_pool2 = MaxPool2D(kerne

l_size=2, stride=2) # 定义一层全连接层，输出维度是10 self.fc = Linear(in_features=980, out_featur

es=10) # 定义网络前向计算过程，卷积后紧接着使用池化层，最后使用全连接层计算最终输出 def forward

(self, inputs): x = self.conv1(inputs)
         x = F.relu(x)
         x = self.max_pool1(x)
         x = self.conv2(x)
         x = F.relu(x)
         x = self.max_pool2(x)
         x = paddle.reshape(x, [x.shape[0], 980])
         x = self.fc(x) #  x = F.softmax(x) return x

class Trainer(object): def __init__(self, model_path, model, optimizer): self.model_path 

= model_path # 模型存放路径  self.model = model # 定义的模型 self.optimizer = optimizer # 优化器

 def save(self): # 保存模型 paddle.save(self.model.state_dict(), self.model_path) def train_s

tep(self, data): images, labels = data # 前向计算的过程 predicts = self.model(images) # 计算损失 

loss = F.cross_entropy(predicts, labels)
        avg_loss = paddle.mean(loss) # 后向传播，更新参数的过程 avg_loss.backward()
        self.optimizer.step()
        self.optimizer.clear_grad() return avg_loss def train_epoch(self, datasets, epoch):

 self.model.train() for batch_id, data in enumerate(datasets()):
            loss = self.train_step(data) # 每训练了1000批次的数据，打印下当前Loss的情况

 if batch_id % 500 == 0:
                print("epoch_id: {}, batch_id: {}, loss is: {}".format(epoch, batch_id, loss.

numpy())) def train(self, train_datasets, start_epoch, end_epoch, save_path): if not os.path.exists(save_path):
            os.makedirs(save_path) for i in range(start_epoch, end_epoch):
            self.train_epoch(train_datasets, i)
            paddle.save(opt.state_dict(), './{}/mnist_epoch{}'.format(save_path,i)+'.pdopt')
            paddle.save(model.state_dict(), './{}/mnist_epoch{}'.format(save_path,i)+'.pdparams')
        self.save()

在开始介绍使用飞桨恢复训练前，先正常训练一个模型，优化器使用Adam，使用动态变化的学习率，学习率从0.01衰减到0.001。每训练一轮后保存一次模型，之后将采用其中某一轮的模型参数进行恢复训练，验证一次性训练和中断再恢复训练的模型表现是否相差不多（训练loss的变化）。

注意进行恢复训练的程序不仅要保存模型参数，还要保存优化器参数。这是因为某些优化器含有一些随着训练过程变换的参数，例如Adam、Adagrad等优化器采用可变学习率的策略，随着训练进行会逐渐减少学习率。这些优化器的参数对于恢复训练至关重要。

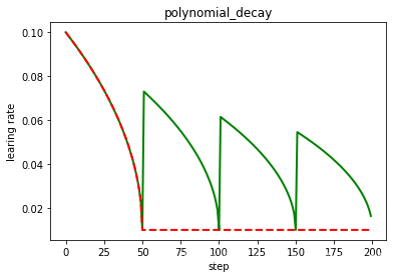
为了演示这个特性，训练程序使用PolynomialDecay API、Adam优化器、学习率以多项式曲线从0.01衰减到0.001。

class paddle.optimizer.lr.PolynomialDecay (learningrate, decaysteps, endlr=0.0001, power=1.0, cycle=False, lastepoch=- 1, verbose=False)

参数说明如下：

• learning_rate (float)：初始学习率，数据类型为Python float。
• decay_steps (int)：进行衰减的步长，这个决定了衰减周期。
• end_lr (float，可选）：最小的最终学习率，默认值为0.0001。
• power (float，可选)：多项式的幂，默认值为1.0。
• last_epoch (int，可选)：上一轮的轮数，重启训练时设置为上一轮的epoch数。默认值为-1，则为初始学习率。
• verbose (bool，可选)：如果是 True，则在每一轮更新时在标准输出stdout输出一条信息，默认值为False。
• cycle (bool，可选)：学习率下降后是否重新上升。若为True，则学习率衰减到最低学习率值时会重新上升。若为False，则学习率单调递减。默认值为False。

PolynomialDecay的变化曲线下图所示：

#在使用GPU机器时，可以将use_gpu变量设置成True use_gpu = True paddle.set_device('gpu:0') 

if use_gpu else paddle.set_device('cpu') import warnings
warnings.filterwarnings('ignore')
paddle.seed(1024)


epochs = 3 BATCH_SIZE = 32 model_path = './mnist.pdparams' train_dataset = MnistDataset(mode='train') 

# 这里为了使每次的训练精度都保持一致，因此先选择了shuffle=False，真正训练时应改为shuffle=True train

_loader = paddle.io.DataLoader(train_dataset, batch_size=BATCH_SIZE, shuffle=False, num_workers=0) 

model = MNIST() # lr = 0.01 total_steps = (int(50000//BATCH_SIZE) + 1) * epochs
lr = paddle.optimizer.lr.PolynomialDecay(learning_rate=0.01, decay_steps=total_steps, end_lr=0.001)
opt = paddle.optimizer.Momentum(learning_rate=lr, parameters=model.parameters())

trainer = Trainer(
    model_path=model_path,
    model=model,
    optimizer=opt
)

trainer.train(train_datasets=train_loader, start_epoch = 0, end_epoch = epochs, save_path='checkpoint')

paddle.load(params_path+'.pdparams') paddle.load(params_path+'.pdopt')

import warnings
warnings.filterwarnings('ignore') # MLP继续训练 paddle.seed(1024)

epochs = 3 BATCH_SIZE = 32 model_path = './mnist_retrain.pdparams' train_dataset = MnistDataset

(mode='train') # 这里为了使每次的训练精度都保持一致，因此先选择了shuffle=False，真正训练时应改为

shuffle=True train_loader = paddle.io.DataLoader(train_dataset, batch_size=BATCH_SIZE, shuffle=False, num_workers=4) 

model = MNIST() # lr = 0.01 total_steps = (int(50000//BATCH_SIZE) + 1) * epochs
lr = paddle.optimizer.lr.PolynomialDecay(learning_rate=0.01, decay_steps=total_steps, end_lr=0.001)
opt = paddle.optimizer.Momentum(learning_rate=lr, parameters=model.parameters())

params_dict = paddle.load('./checkpoint/mnist_epoch0.pdparams')
opt_dict = paddle.load('./checkpoint/mnist_epoch0.pdopt') # 加载参数到模型 model.set_state_dict(params_dict)
opt.set_state_dict(opt_dict)

trainer = Trainer(
    model_path=model_path,
    model=model,
    optimizer=opt
) # 前面训练模型都保存了，这里save_path设置为新路径，实际训练中保存在同一目录就可以 trainer.tra

in(train_datasets=train_loader,start_epoch = 1, end_epoch = epochs, save_path='checkpoint_con')

epoch_id: 1, batch_id: 0, loss is: [2.28961]
epoch_id: 1, batch_id: 500, loss is: [2.3036923]
epoch_id: 1, batch_id: 1000, loss is: [2.246863]
epoch_id: 1, batch_id: 1500, loss is: [1.2581751]
epoch_id: 2, batch_id: 0, loss is: [1.6448064]
epoch_id: 2, batch_id: 500, loss is: [0.85551864]
epoch_id: 2, batch_id: 1000, loss is: [0.7411902]
epoch_id: 2, batch_id: 1500, loss is: [0.3651021]

paddle.save(opt.state_dict(), 'model.pdopt')
paddle.save(model.state_dict(), 'model.pdparams')

model_dict = paddle.load("model.pdparams")
opt_dict = paddle.load("model.pdopt")

model.set_state_dict(model_dict) opt.set_state_dict(opt_dict)